Кумулятивний частотний аналіз
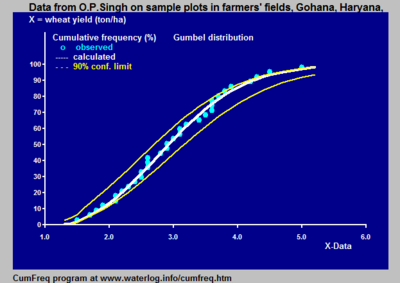
Кумуляти́вний частóтний анáліз – це аналіз частоти появи значень явища, менших за еталонне значення. Явище може залежати від часу або простору. Кумулятивну частоту також називають частотою неперевищення.
Кумулятивний частотний аналіз виконується, щоб отримати уявлення про те, як часто певне явище (особливість) є нижчим за певне значення. Це може допомогти в описі або поясненні ситуації, в якій бере участь явище, або в плануванні заходів, наприклад, для захисту від повеней. [1]
Цю статистичну техніку можна використовувати, щоб побачити, наскільки ймовірна така подія, як повінь, повториться в майбутньому, виходячи з того, як часто це відбувалося в минулому. Його можна адаптувати, щоб внести такі зміни, як зміна клімату, що спричинить вологі зими та сухіше літо.
Частотний аналіз [2] – це аналіз того, як часто спостережуване явище відбувається в певному діапазоні.
Частотний аналіз застосовується до запису довжини N спостережуваних даних X 1, X 2, X 3 . . . X N на змінне явище X . Запис може залежати від часу (наприклад, кількість опадів, виміряних в одній точці) або залежати від простору (наприклад, урожайність сільськогосподарських культур на території) чи іншим чином.
Кумулятивна частота MXr еталонного значення Xr є частотою, на яку спостережувані значення X менші або дорівнюють Xr .
Відносну кумулятивну частоту Fc можна розрахувати за формулою:
де N – кількість даних
Коротко цей вираз можна позначити так: Fc = M / N Коли Xr = Xmin, де Xmin є унікальним мінімальним значенням, яке спостерігається, виявляється, що Fc = 1/N, оскільки M = 1 . З іншого боку, коли Xr = Xmax, де Xmax є унікальним максимальним значенням, яке спостерігається, виявляється, що Fc = 1, оскільки M = N . Отже, коли Fc = 1 це означає, що Xr є значенням, за яким усі дані менші або дорівнюють Xr .
У відсотках рівняння виглядає так:
Кумулятивну ймовірність Pc X бути меншим або рівним Xr можна оцінити кількома способами на основі кумулятивної частоти M .
Одним із способів є використання відносної кумулятивної частоти Fc як оцінки.
Іншим способом є врахування можливості того, що в рідкісних випадках X може приймати значення, більші за спостережуваний максимум X max . Це можна зробити, поділивши кумулятивну частоту M на N +1 замість N . Тоді оцінка стає:
Існують також інші пропозиції щодо знаменника (див. позиції на графіку ).

Оцінка ймовірності полегшується шляхом ранжування даних.
Коли спостережувані дані X розташовані в порядку зростання ( X1 ≤ X2 ≤ X3 ≤ ⋯ ≤ XN, мінімум першим і максимум останнім), а Ri є ранговим номером спостереження Xi, де доповнення i вказує порядковий номер у діапазоні зростаючих даних, тоді кумулятивну ймовірність можна оцінити за допомогою:
Коли, з іншого боку, спостережувані дані з X розташовані в порядку спадання, максимум першим і мінімум останнім, а Rj є ранговим номером спостереження Xj, кумулятивну ймовірність можна оцінити за допомогою:

Щоб представити кумулятивний розподіл частот як неперервне математичне рівняння замість дискретного набору даних, можна спробувати підігнати кумулятивний розподіл частот до відомого кумулятивного розподілу ймовірностей. [2] [3]У разі успіху відомого рівняння достатньо, щоб повідомити про розподіл частот, і таблиця даних не потрібна. Крім того, рівняння допомагає інтерполяції та екстраполяції. Однак слід бути обережним з екстраполяцією кумулятивного розподілу частот, оскільки це може бути джерелом помилок. Однією з можливих помилок є те, що частотний розподіл більше не відповідає обраному розподілу ймовірностей за межами діапазону спостережуваних даних.
Будь-яке рівняння, яке дає значення 1 при інтегруванні від нижньої межі до верхньої межі, що добре узгоджується з діапазоном даних, може використовуватися як розподіл ймовірностей для підгонки. Зразок розподілу ймовірностей, який можна використовувати, можна знайти в розділі розподілу ймовірностей.
Розподіл ймовірностей можна підібрати декількома методами, [2] наприклад:
- параметричний метод, що визначає такі параметри, як середнє значення та стандартне відхилення від даних X за допомогою методу моментів, методу максимальної правдоподібності та методу ймовірно зважених моментів .
- метод регресії, що лінеаризує розподіл ймовірностей через перетворення та визначає параметри з лінійної регресії перетвореного Pc (отриманого в результаті ранжування) на перетворених даних X.
Застосування обох типів методів
- нормальний розподіл, логарифмічний нормальний розподіл, логістичний розподіл, логістичний розподіл, експоненціальний розподіл, розподіл Фреше, розподіл Гамбеля, розподіл Парето, розподіл Вейбулла та інші
часто показує, що ряд розподілів добре відповідає даним і не дає суттєво відмінних результатів, тоді як відмінності між ними можуть бути невеликими порівняно з шириною довірчого інтервалу. [2] Це показує, що може бути важко визначити, який розподіл дає кращі результати. Наприклад, приблизно нормально розподілені набори даних можуть бути підігнані до великої кількості різних розподілів ймовірностей. [4], тоді як негативно викривлені розподіли можуть бути підігнані до квадратичних нормальних і дзеркальних розподілів Гамбеля. [5]

Іноді можливо підібрати один тип розподілу ймовірностей до нижньої частини діапазону даних, а інший тип – до вищої частини, розділених точкою розриву, завдяки чому загальна відповідність покращується.
На малюнку наведено приклад корисного впровадження такого непостійного розподілу для даних про кількість опадів у північному Перу, де клімат залежить від поведінки течії Ель-Ніньйо в Тихому океані. Коли Ніньйо простягається на південь від Еквадору і впадає в океан уздовж узбережжя Перу, клімат Північного Перу стає тропічним і вологим. Коли Ніньйо не досягає Перу, клімат напівпосушливий. З цієї причини більша кількість опадів має інший розподіл частоти, ніж менша кількість опадів. [6]
Коли кумулятивний розподіл частот виводиться із запису даних, можна поставити під сумнів, чи можна його використовувати для прогнозів. [7] Наприклад, враховуючи розподіл річкових стоків за 1950–2000 роки, чи можна використовувати цей розподіл для прогнозування того, як часто буде перевищуватися певний річковий стік у 2000–50 роках? Відповідь - так, за умови, що умови середовища не зміняться. Якщо умови навколишнього середовища змінюються, наприклад, зміни в інфраструктурі вододілу річки або в структурі опадів через кліматичні зміни, прогноз на основі історичних даних піддається систематичній помилці. Навіть якщо систематичної помилки немає, може бути випадкова помилка, тому що випадково спостережувані скиди протягом 1950–2000 років могли бути вищими або нижчими за норму, тоді як, з іншого боку, скиди з 2000 по 2050 роки випадково можуть бути нижчими або вище норми. Питання навколо цього були досліджені в книзі «Чорний лебідь» .


Теорія ймовірностей може допомогти оцінити діапазон, в якому може бути випадкова помилка. У випадку кумулятивної частоти є лише дві можливості: певне контрольне значення X перевищено або не перевищено. Сума частоти перевищення та сукупної частоти становить 1 або 100%. Отже, біноміальний розподіл можна використовувати для оцінки діапазону випадкової помилки.
Відповідно до нормальної теорії біноміальний розподіл можна наближено і для великих N стандартне відхилення Sd можна обчислити наступним чином:
де Pc – кумулятивна ймовірність, а N – кількість даних. Видно, що стандартне відхилення Sd зменшується зі збільшенням кількості спостережень N.
Для визначення довірчого інтервалу Pc використовується T-критерій Стьюдента (t ). Значення t залежить від кількості даних та рівня довіри до оцінки довірчого інтервалу. Тоді нижня (L) і верхня (U) довірчі межі Pc у симетричному розподілі знаходяться з:
Це відоме як інтервал Вальда. [8] Однак біноміальний розподіл є лише симетричним навколо середнього значення, коли Pc = 0.5, але він стає асиметричним і дедалі більше перекошеним, коли Pc наближається до 0 або 1. Таким чином, шляхом наближення Pc і 1− Pc можна використовувати як вагові коефіцієнти при призначенні t. Sd до L і U :
звідки видно, що ці вирази для Pc = 0,5 такі самі, як і попередні.
| N = 25, Pc = 0.8, Sd = 0.08, рівень довіри 90%, t = 1.71, L = 0.58, U = 0.85 Таким чином, з достовірністю 90% виявлено, що 0,58 < Pc < 0.85 Тим не менш, існує 10% ймовірність того, що Pc < 0.58 або Pc > 0.85 |
- Відомо, що інтервал Вальда працює погано. [9] [10] [11]
- Інтервал оцінок Вільсона [12] забезпечує довірчий інтервал для біноміальних розподілів на основі тестів оцінок і має краще охоплення вибірки, див. [13] і довірчий інтервал біноміальної пропорції для більш детального огляду.
- Замість «інтервалу балів Вільсона» також можна використовувати «інтервал Вальда» за умови врахування наведених вище вагових факторів.

Період повернення T визначається як:
і вказує на очікувану кількість спостережень, які необхідно виконати знову, щоб знайти значення досліджуваної змінної, що перевищує значення, використане для T.Верхня ( T U ) і нижня ( T L ) довірчі межі періодів повернення можна знайти відповідно як:
Для екстремальних значень досліджуваної змінної U наближається до 1, і невеликі зміни U викликають значні зміни T U . Отже, розрахунковий період повернення екстремальних значень піддається великій випадковій похибці. Крім того, знайдені довірчі інтервали відповідають довгостроковому прогнозу. Для короткострокових прогнозів довірчі інтервали U−L і TU−TL можуть бути ширшими. Разом із обмеженою достовірністю (менше 100%), яка використовується в t-критерії, це пояснює, чому, наприклад, 100-річна кількість опадів може випадати двічі за 10 років.

Суворе поняття періоду повторення насправді має сенс лише тоді, коли воно стосується явища, що залежить від часу, наприклад точкових опадів. Тоді період повернення відповідає очікуваному часу очікування, доки перевищення не відбудеться знову. Період повернення має таку ж величину, як і час, для якого кожне спостереження є репрезентативним. Наприклад, коли спостереження стосуються добових опадів, період повторення виражається в днях, а для річних опадів – роками.
На рисунку показано варіацію, яка може виникнути при отриманні вибірок змінної, яка відповідає певному розподілу ймовірностей. Дані надав Бенсон. [1]
Довірчий пояс навколо експериментальної кумулятивної кривої частоти або періоду повернення дає враження про область, у якій можна знайти справжній розподіл.
Крім того, це пояснює, що експериментально знайдений найкращий розподіл ймовірностей може відхилятися від справжнього розподілу.

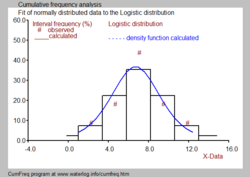
Спостережувані дані можуть бути організовані в класи або групи з порядковим номером k . Кожна група має нижню межу ( Lk ) і верхню межу ( Uk ). Якщо клас ( k ) містить mk даних, а загальна кількість даних дорівнює N, тоді відносна частота класу або групи визначається з:
або коротко:
або у відсотках:
Представлення всіх частот класу дає частотний розподіл або гістограму . Гістограми, навіть створені з одного запису, відрізняються для різних обмежень класу.
Гістограма також може бути отримана з підігнаного кумулятивного розподілу ймовірностей:
Може бути різниця між Fgk і Pgk через відхилення спостережуваних даних від підігнаного розподілу (див. синій малюнок).
Часто бажано поєднати гістограму з функцією щільності ймовірності, як показано на чорно-білому зображенні.
- Довірчий інтервал біноміальної пропорції
- Кумулятивна функція розподілу
- Розподільна арматура
- Частота (статистика)
- Частота перевищення
- кумулятивні обсяги (логістика)
- ↑ а б Benson, M.A. 1960. Characteristics of frequency curves based on a theoretical 1000-year record. In: T.Dalrymple (ed.), Flood frequency analysis. U.S. Geological Survey Water Supply paper 1543-A, pp. 51–71
- ↑ а б в г Frequency and Regression Analysis. Chapter 6 in: H.P. Ritzema (ed., 1994), Drainage Principles and Applications, Publ. 16, pp. 175–224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN 90-70754-33-9 . Free download from the webpage under nr. 12, or directly as PDF :
- ↑ David Vose, Fitting distributions to data
- ↑ Example of an approximately normally distributed data set to which a large number of different probability distributions can be fitted,
- ↑ Left (negatively) skewed frequency histograms can be fitted to square normal or mirrored Gumbel probability functions.
- ↑ CumFreq, a program for cumulative frequency analysis with confidence bands, return periods, and a discontinuity option. Free download from :
- ↑ Silvia Masciocchi, 2012, Statistical Methods in Particle Physics, Lecture 11, Winter Semester 2012 / 13, GSI Darmstadt.
- ↑ Wald, A.; J. Wolfowitz (1939). Confidence limits for continuous distribution functions. The Annals of Mathematical Statistics. 10 (2): 105—118. doi:10.1214/aoms/1177732209.
- ↑ Ghosh, B.K (1979). A comparison of some approximate confidence intervals for the binomial parameter. Journal of the American Statistical Association. 74 (368): 894—900. doi:10.1080/01621459.1979.10481051.
- ↑ Blyth, C.R.; H.A. Still (1983). Binomial confidence intervals. Journal of the American Statistical Association. 78 (381): 108—116. doi:10.1080/01621459.1983.10477938.
- ↑ Agresti, A.; B. Caffo (2000). Simple and effective confidence intervals for pro- portions and differences of proportions result from adding two successes and two failures. The American Statistician. 54 (4): 280—288. doi:10.1080/00031305.2000.10474560.
- ↑ Wilson, E.B. (1927). Probable inference, the law of succession, and statistical inference. Journal of the American Statistical Association. 22 (158): 209—212. doi:10.1080/01621459.1927.10502953.
- ↑ Hogg, R.V. (2001). Probability and statistical inference (вид. 6th). Prentice Hall, NJ: Upper Saddle River.